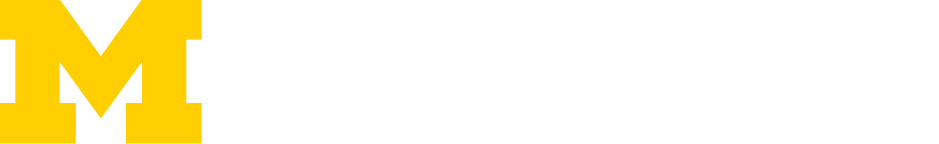- Optimal Experimental Design
- Sequential Optimal Experimental Design
- Uncertainty Quantification for Machine Learning Models
- Uncertainty Quantification for Engineering Applications
Optimal Experimental Design
Experiments are often expensive, time-consuming, and even dangerous. However, not all experiments are equal, and some can produce more valuable data than others. Identifying and executing these good experiments can lead to substantial resource savings.
We develop mathematical frameworks and computational algorithms for optimal experimental design (OED), and seek to address questions such as:
- Under what condition should we conduct an experiment?
- What quantities should we probe?
- Where and when should we take measurements?
- Have we gathered enough data, or should continue with more experiments?
OED is a form of decision-making under uncertainty. For example, when our experimental goal is to learn about model parameters fromnoisy measurements, a possible approach involves finding the design decision maximizing the expected information gain (mutual information).
There are many challenges associated with finding the optimal design, including the need for optimization routines to accommodate noisy objectives, repeated Bayesian inferences under different scenarios, and all while wrapping around an often computationally intensive, high-dimensional nonlinear physics-based forward model.
Example: hydrogen-oxygen ignition (doi: 10.1016/j.jcp.2012.08.013)
- Design: initial temperature and equivalence ratio
- Measure: ignition delay times
- Infer: Arrhenius kinetic parameters
Below are expected utility contours approximated from using the full physical model (left), and a polynomial chaos surrogate model that greatly accelerate the computations (right); they show excellent agreement.
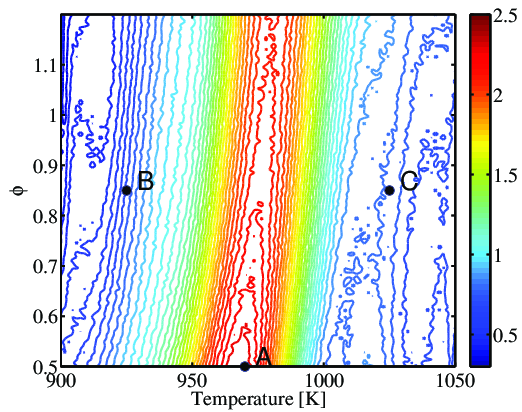
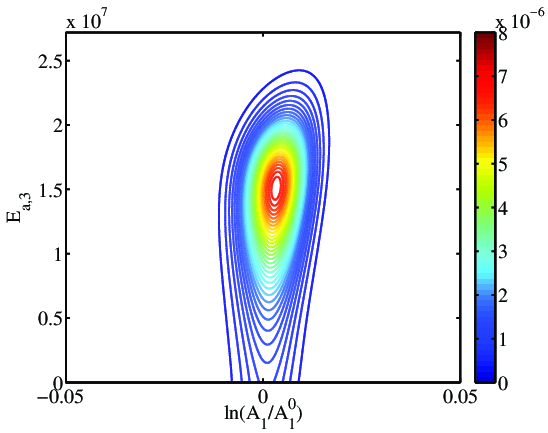
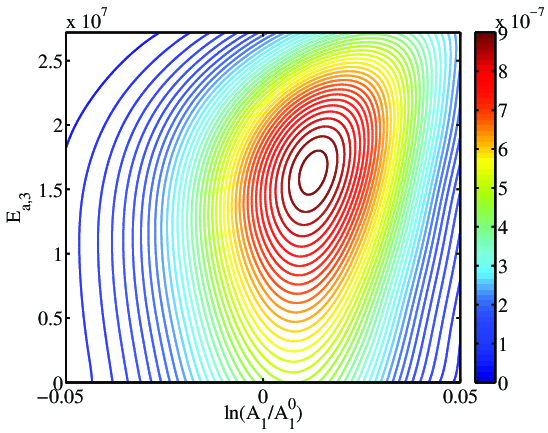
Three experiments are simulated (at designs A, B, and C in figure above). Bayesian inference is performed and posterior densities are shown below. Designs A (which has the highest expected utility value) produces the “tightest” posterior (left), reflecting a larger reduction in uncertainty and increased confidence for estimating these parameters.
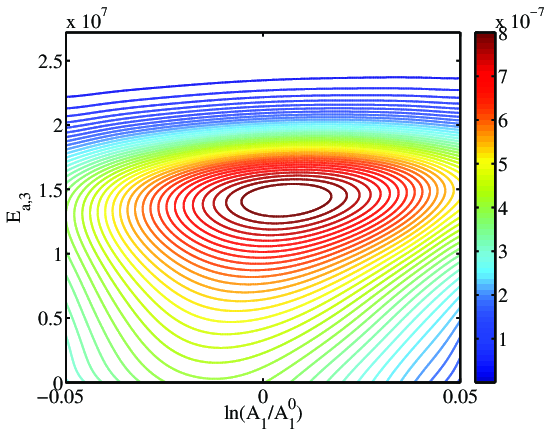
Sequential Optimal Experimental Design
Coming soon!
Uncertainty Quantification for Machine Learning Models
Coming soon!
Uncertainty Quantification in Engineering Applications
Uncertainty quantification (UQ) plays a crucial role in engineering and science. UQ is particularly important for the learning process, by providing a principled framework for interactions among theory, models, and data.
Example: reactive flows inside a scramjet combustor (doi: 0.2514/1.J056278)
Scramjets are propulsive systems that can enable efficient and stable operations under hypersonic flight conditions (Mach 5+). For instance, the figure below shows the flight test payload from the Hypersonic International Flight Research Experimentation (HIFiRE) program.
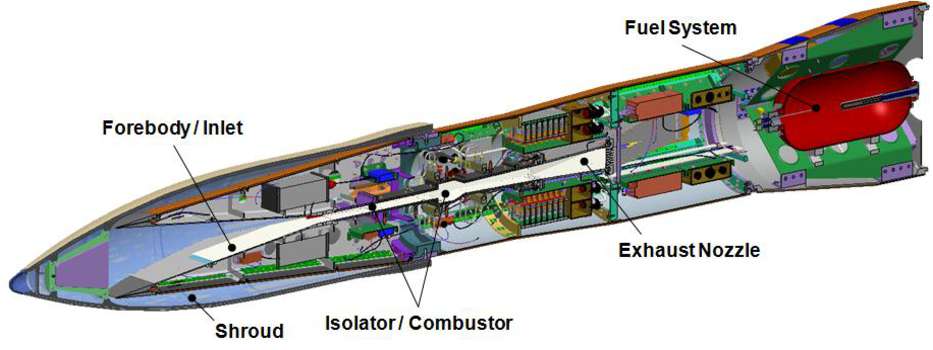
Designing scramjet engines requires both accurate flow simulations as well as UQ. Enabling UQ for expensive simulations of turbulent supersonic reactive flows faces many computational challenges. Techniques such as global sensitivity analysis, surrogate modeling, compressive sensing, efficient Bayesian calibration, and multilevel multifidelity sampling are needed to make UQ analysis possible. Below is an illustration of the predictive uncertainty (blue contours) of Mach number at select vertical stations of the combustor section. Such information would be valuable for finding optimal scramjet designs that are also robust and reliable.