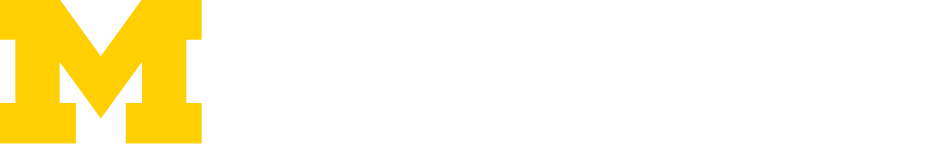Teaching

This course introduces the theory and practice of the finite element method. One-dimensional, two-dimensional, and three-dimensional elements are studied, including structural elements. Primary fields of applications are strength of materials (deformation and stress analysis) and dynamics and vibrations. Classes involve extensive use of commercial finite element software packages, through computer labs and graded assignments.

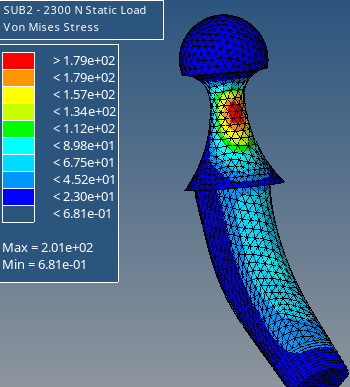
This course presents a mathematical introduction of partial differential equations (PDEs) to conduct graduate-level research in mechanical engineering. We will start with classical concepts for solving PDEs, including the separation of variables, Sturm-Liouville problems, Green’s functions, and method of characteristics. We will then provide a brief introduction to the finite difference method, followed by advanced topics involving PDE-based tasks such as uncertainty quantification, inverse problems, and PDE-constrained optimization. Throughout the course, applications in mechanical engineering will be used as examples to derive and analyze their associated PDEs.

This course presents an introduction of computational and data-driven methods for conducting graduate-level engineering research. The theme of the course centers around scientific learning, approached as an inverse problem. We will investigate broad categories of non-probabilistic, probabilistic, and data-driven approaches for solving and accelerating the solution of inverse problems, such as linear and nonlinear regression with regularization and cross-validation; Bayesian inference using Markov chain Monte Carlo and variational Bayes; data-driven modeling with polynomial chaos, Karhunen-Loeve expansions, Gaussian processes, and deep neural networks. Lastly, we will introduce strategies for “what new data should we acquire?” via optimal experimental design.